Advertisements
Advertisements
Question
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
Solution
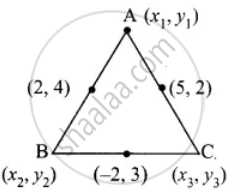
Let the vertices of the ΔABC be A(x1 y1), B(x2, y2) and C(x3, y3)
Mid−point of AB = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(2, 4) = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
`(x_1 + x_2)/2` = 2
⇒ x1 + x2 = 4 → (1)
`(y_1 + y_2)/2` = 4
⇒ y1 + y2 = 8 → (2)
Mid−point of BC = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
(−2, 3) = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
`(x_2 + x_3)/2` = − 2
⇒ x2 + x3 = − 4 → (3)
`(y_2 + y_3)/2` = 3
⇒ y2 + y3 = 6 → (4)
Mid−point of AC = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
(5, 2) = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
`(x_1 + x_3)/2` = 5
⇒ x1 + x3 = 10 → (5)
`(y_1 + y_3)/2` = 2
⇒ y1 + y3 = 4 → (6)
By adding (1) + (3) + (5) we get
2x1 + 2x2 + 2x3 = 4 – 4 + 10
2(x1 + x2 + x3) = 10
⇒ x1 + x2 + x3 = 5
From (1) x1 + x2 = 4
⇒ 4 + x3 = 5
x3 = 5 – 4 = 1
∴ The vertices of the ΔABC are A(9, 3) B(– 5, 5), C(1, 1)
From (3) x2 + x3 = – 4
⇒ x1 + (– 4) = 5
x1 = 5 + 4 = 9
From (5) ⇒ x1 + x3 = 8
x2 + 10 = 5
x2 = 5 – 10 = – 5
∴ x1 = 9, x2 = – 5, x3 = 1
By adding (2) + (4) + (6) we get
2y1 + 2y2 + 2y3 = 8 + 6 + 4
2(y1 +y2 + y3) = 18
⇒ y1 + y2 + y3 = 9
From (2) ⇒ y1 + y2 = 8
8 + y3 = 9
⇒ y3 = 9 – 8
= 1
From (4)
y2 + y3 = 6
⇒ y1 + 6 = 9
y1 = 9 – 6
= 3
From (6)
y1 + y3 = 4
⇒ y2 + 4
= 9
y2 = 9 – 4
= 5
∴ y1 = 3, y2 = 5, y3 = 1
APPEARS IN
RELATED QUESTIONS
A(–1, 0), B(1, 3) and D(3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–2, –5), Q(4, 3), a : b = 3 : 4
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(2, 6), Q(–4, 1), a : b = 1 : 2
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Find the midpoint of the line segment joining the following pair of point :
(a+b, b-a) and (a-b, a+b)
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the co-ordinates of centroid of a triangle if points D(–7, 6), E(8, 5) and F(2, –2) are the mid-points of the sides of that triangle.
