Advertisements
Advertisements
Question
Find the coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Solution
Let, M(x, y) be the midpoint of line PQ.
P(0, 6) = (x1, y1), Q (12, 20) = (x2, y2)
By the midpoint formula,
x =
=
=
= 6
y =
=
=
= 13
The coordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20) are M(6, 13).
APPEARS IN
RELATED QUESTIONS
A(2, 5), B(1, 0), C(−4, 3) and D(–3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Two vertices of a triangle are (1, 4) and (3, 1). If the centroid of the triangle is the origin, find the third vertex.
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
The coordinates of the end points of the diameter of a circle are (3, 1) and (7, 11). Find the coordinates of the centre of the circle.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The centre of a circle is (−4, 2). If one end of the diameter of the circle is (−3, 7) then find the other end
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, −7) is
The mid-point of the line joining (−a, 2b) and (−3a, −4b) is
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
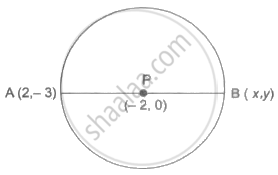
Given: A
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
⇒
⇒ x =
⇒ x = – 6
and
⇒
⇒ y = 3
Hence coordinates of B is (– 6, 3).
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x =
y =
∴ Co-ordinates of midpoint P are
