Advertisements
Advertisements
Question
Find the ratio in which the line segment joining the points A(3, 8) and B(–9, 3) is divided by the Y– axis.
Solution
Let C be a point on Y-axis which divides seg AB in the ratio m: n.
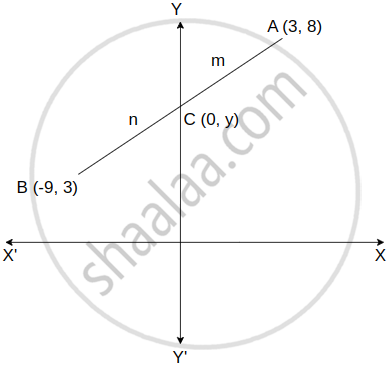
Point C lies on the Y-axis. Thus, its x coordinate is 0.
Let C = (0, y)
∴ x1 = −9, y1 = 3, x2 = 3, y2 = 8
∴ By section formula,
`"x" = ("mx"_2 + "nx"_1)/"m + n"`
∴ `0 = "m × 3 + n × −9"/"m + n"`
∴ `0 = "3m − 9n"/"m + n"`
∴ 0 = 3m − 9n
∴ 9n = 3m
∴ `"m"/"n" = 9/3`
∴ `"m"/"n" = 3/1`
∴ m : n = 3 : 1
Y-axis divides the seg AB in the ratio 3: 1.
APPEARS IN
RELATED QUESTIONS
In Fig. 14.36, a right triangle BOA is given C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.

We have a right angled triangle,`triangle BOA` right angled at O. Co-ordinates are B (0,2b); A (2a, 0) and C (0, 0).
The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the coordinates of the fourth vertex.
Prove that the points (4, 5) (7, 6), (6, 3) (3, 2) are the vertices of a parallelogram. Is it a rectangle.
The points A(2, 0), B(9, 1) C(11, 6) and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
If the point P(x, 3) is equidistant from the point A(7, −1) and B(6, 8), then find the value of x and find the distance AP.
If A(−3, 5), B(−2, −7), C(1, −8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
Write the perimeter of the triangle formed by the points O (0, 0), A (a, 0) and B (0, b).
Write the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 : 5.
Find the value of a so that the point (3, a) lies on the line represented by 2x − 3y + 5 = 0
The ratio in which the line segment joining P (x1, y1) and Q (x2, y2) is divided by x-axis is
A line intersects the y-axis and x-axis at P and Q , respectively. If (2,-5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
Find the coordinates of the point of intersection of the graph of the equation x = 2 and y = – 3
Signs of the abscissa and ordinate of a point in the second quadrant are respectively.
Which of the points P(0, 3), Q(1, 0), R(0, –1), S(–5, 0), T(1, 2) do not lie on the x-axis?
Find the coordinates of the point which lies on x and y axes both.
The distance of the point (3, 5) from x-axis (in units) is ______.
Assertion (A): Mid-point of a line segment divides the line segment in the ratio 1 : 1
Reason (R): The ratio in which the point (−3, k) divides the line segment joining the points (− 5, 4) and (− 2, 3) is 1 : 2.
