Advertisements
Advertisements
Question
Determine whether the given point is collinear.
L(1,2), M(5,3) , N(8,6)
Solution
L(1,2), M(5,3) , N(8,6)
Slope of LM
\[= \frac{3 - 2}{5 - 1} = \frac{1}{4}\]
Slope of MN = \[\frac{6 - 3}{8 - 5} = \frac{3}{3} = 1\]
Thus, the slope of LM not equal to slope MN.
So, the given points are not collinear.
APPEARS IN
RELATED QUESTIONS
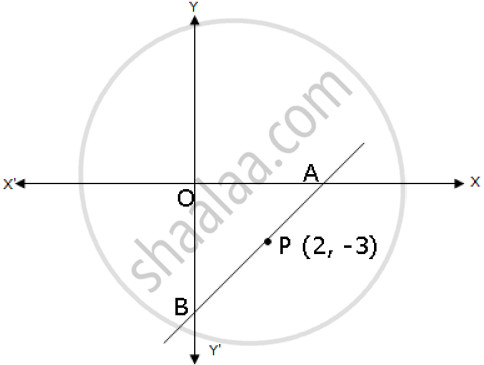
A and B are two points on the x-axis and y-axis respectively. P (2, −3) is the midpoint of AB. Find the:
(1) coordinates of A and B
(2) slope of line AB.
(3) an equation of line AB.
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Find the slope of the line which is parallel to x + 2y + 3 = 0
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
60°
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
90°
Find the slope of the lines passing through the given point.
P (–3, 1) , Q (5, –2)
If A(1, –1), B(0, 4), C(–5, 3) are vertices of a triangle then find the slope of each side.
Find the slope of a line, correct of two decimals, whose inclination is 45°
Find the slope of a line parallel to the given line 3x-2y = 5
Find the slope of a line parallel to the given line 5x + 2y = 11
Find the slope of a line passing through the points (x, 9) and (12, 6) is `(-1)/3 = ("y"_2 - "y"_1)/("x"_2 - "x"_1)`
Find m if the slope of the line passing through the point (-7,5) and (2,m) is `1/3`
Find the slope of the line passing through the points M(4,0) and N(-2,-3).
Find the slope of the line passing through the points A(6, -2) and B(–3, 4).
Find the Slope of the line having inclination 45°.
Given that (a, 2a) lies on line`(y)/(2) = 3 - 6`.Find the value of a.
Prove that A(4, 3), B(6, 4), C(5, 6) and D(3, 5) are the angular points of a square.
If A(6, 1), B(8, 2), C(9, 4) and D(7, 3) are the vertices of `square`ABCD, show that `square`ABCD is a parallelogram.
Solution:
Slope of line = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
∴ Slope of line AB = `(2 - 1)/(8 - 6) = square` .......(i)
∴ Slope of line BC = `(4 - 2)/(9 - 8) = square` .....(ii)
∴ Slope of line CD = `(3 - 4)/(7 - 9) = square` .....(iii)
∴ Slope of line DA = `(3 - 1)/(7 - 6) = square` .....(iv)
∴ Slope of line AB = `square` ......[From (i) and (iii)]
∴ line AB || line CD
∴ Slope of line BC = `square` ......[From (ii) and (iv)]
∴ line BC || line DA
Both the pairs of opposite sides of the quadrilateral are parallel.
∴ `square`ABCD is a parallelogram.
If the lines 7y = ax + 4 and 2y = 3 − x, are parallel to each other, then the value of ‘a’ is:
