Advertisements
Advertisements
Question
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
60°
Solution
60°
\[m = \tan60° = \sqrt{3}\]
Thus, slope = \[\sqrt{3}\]
APPEARS IN
RELATED QUESTIONS
(−2, 4), (4, 8), (10, 7) and (11, –5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
Show that the points P(a, b + c), Q(b, c + a) and R(c, a + b) are collinear.
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Plot the points A(1, 1), B(4, 7) and C(4, 10) on a graph paper. Connect A and B and also A and C.
Which segment appears to have the steeper slope, AB or AC?
Justify your conclusion by calculating the slopes of AB and AC.
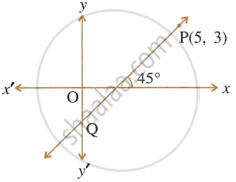
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
Find the slope of the line which is parallel to x + 2y + 3 = 0
Find the slope of the line which is perpendicular to `x/3 - 2y = 4`
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Find the slope of the lines passing through the given point.
E(–4, –2) , F (6, 3)
If A(1, –1), B(0, 4), C(–5, 3) are vertices of a triangle then find the slope of each side.
Find k, if B(k, –5), C (1, 2) and slope of the line is 7.
Find the slope of a line, correct of two decimals, whose inclination is 60°
Find the slope of a line passing through the points (x, 9) and (12, 6) is `(-1)/3 = ("y"_2 - "y"_1)/("x"_2 - "x"_1)`
Verify whether the following points are collinear or not:
A(1, –3), B(2, –5), C(–4, 7).
Find the slope of the line passing through the points A(6, -2) and B(–3, 4).
Find the slope of the line passing through the points A(4,7) and B(2,3).
Write the equation of a line passing through the point P (0,6) and having slope 6/7.
A line passing through the points (a, 2a) and (- 2, 3) is perpendicular to the line 4a + 3y + 5 = 0. Find the value of a.
Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD
What is the name of the point of intersection of coordinate axes?
