Advertisements
Advertisements
Question
Write the equation of a line passing through the point P (0,6) and having slope 6/7.
Solution
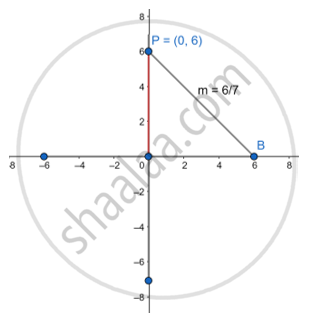
Let P (0,6) =(x1,y1)
y-y1=m(x-x1)
∴ `"y"-6 = 6/7 ("x"-0)`
∴ `"y"-6 = 6/7"x"`
∴7y-42=6x
Slope-intercept equation ⇒ `6"x-7y"=42`
APPEARS IN
RELATED QUESTIONS
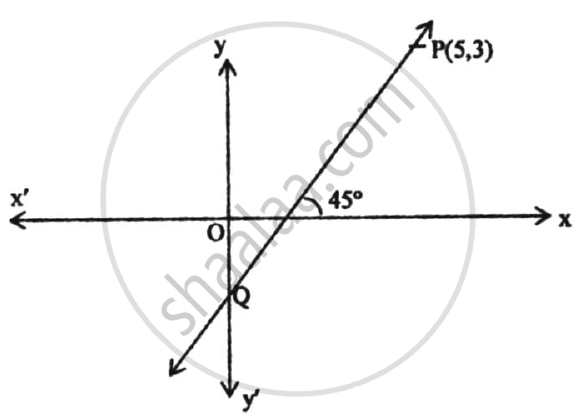
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.
Find the value(s) of k so that PQ will be parallel to RS. Given : P(2, 4), Q(3, 6), R(8, 1) and S(10, k)
Find the slope of the line which is parallel to x + 2y + 3 = 0
Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Find the slope of the lines passing through the given point.
P (–3, 1) , Q (5, –2)
Find the slope of the lines passing through the given point.
C (5, –2) , D (7, 3)
Find the slope of the lines passing through the given point.
L (–2, –3) , M (–6, –8)
Determine whether the following point is collinear.
D(–2, –3), E(1, 0), F(2, 1)
Determine whether the given point is collinear.
\[P\left( 1, 2 \right), Q\left( 2, \frac{8}{5} \right), R\left( 3, \frac{6}{5} \right)\]
Find the slope of the diagonals of a quadrilateral with vertices A(1, 7), B(6, 3), C(0, –3) and D(–3, 3).
Find the slope of a line, correct of two decimals, whose inclination is 45°
Find the slope of a line parallel to the given line 3x-2y = 5
Find the slope of a line parallel to the given line 4x-2y = 3
Find the value of a line perpendicular to the given line 5x+2y-9 = 0
Find the slope and the y-intercept of the following line 2x + 3y = 12
The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the
Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD
If the lines 7y = ax + 4 and 2y = 3 − x, are parallel to each other, then the value of ‘a’ is:
