Question

The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the

Answer 1

Let AD, BE and CF be the three altitudes of ΔABC then
AD ⊥ BC
BE  ⊥ CA
and CF ⊥ AB.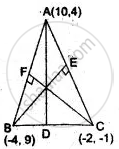

Slope of BC = `(-1 - 9)/(-2 + 4)` = -5
Since AD ⊥ BC
Slope of BC x slope of AD = -1
Slope of AD = `(-1)/(-5) = (1)/(5)`
Therefore AD ⊥ BC
Since, AD passes through A(10, 4)
So, equation of AD is
y - y₁ = m (x - x₁)
y - 4 = `(1)/(5) (x - 10)`
⇒ 5y - 20 = x - 10
⇒ x - 5y + 10 = 0                ...(i)
Now , Slope of AC = `(4 + 1)/(10 + 2) = (-5)/(12)`
since BE ⊥ AC
Slope of BE x Slope of AC = -1
So, Slope of BE = `(-1 xx 12)/(5) = -(12)/(5)`.
Equation of BE which passes through B(-4, 9) is
y - y₁ = m(x - x₁)
y - 9 = `(-12)/(5)(x + 4)`
or 12x + 5y + 3 = 0        ...(ii)
Slope of AB x Slope of CF = -1
⇒ `-(5)/(14)` x Slope of CF = -1
⇒ Slope of CF = `(14)/(5)`
Equation of CF which passes through C(-2, -1) is 
y - y₁ = m (x - x₁)
y + 1 = `(14)/(5) (x + 2)`
⇒ 14x - 5y + 23 = 0           ...(iii)
Thus, the equation of altitudes of ΔABC are
x - 5y + 10 = 0
12x + 5y + 3 = 0
and 14x - 5y + 23 = 0.