Advertisements
Advertisements
Question
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
Solution
Let CD be the line mirror with slope m1.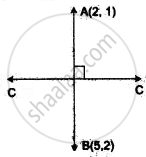
Now the slope of the line joining A(2, 1) and B(5, 2).
m2 =
Since CD ⊥ AB
So, m1m2 = -1
⇒
⇒ m1 = -3.
Now mid point of AB =
Equation of the mirror CD,
y = y1 = m(x - x1)
⇒
⇒
⇒ 2y - 3 = -6x + 21
⇒ 6x + 2y - 3 - 21 = 0
⇒ 6x + 2y - 24 = 0
or 3x + y - 12 = 0.
APPEARS IN
RELATED QUESTIONS
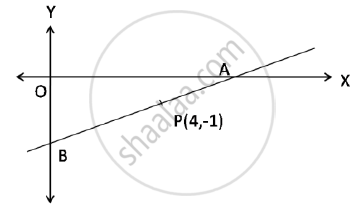
A line AB meets X – axis at A and Y –axis at B. P (4, -1) divides AB in the ratio 1 : 2.
1) Find the coordinates of A and B.
2) Find the equation of the line through P and perpendicular to AB.
Solve the following inequation and represent the solution set on the number line 2x – 5 <= 5x + 4 < 11, where x ∈ I
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(1, 3)
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(–5, 0)
Write down the equation of the line whose gradient is
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
Find the equation of a line passing through (8,3) and making an angle of 45° with the positive direction of the y-axis.
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
