Advertisements
Advertisements
Question
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
Solution
Equation of the line passing through AC is
(y - 3) = `((a - 3)/(5 - a))(x - a)`
As if A, B and C are callinear than B will satisfy it, i.e.,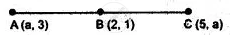
(1 - 3) = `((a - 3)/(5 - a)) (2 - a)`
-2(5 - a) = (a - 3) (2 - a)
-10 + 2a = 2a - 6 - a2 + 3a
a2 - 3a - 4 = 0
a2 - 4a +a - 4 = 0
a(a - 4) + 1 (a - 4) = 0
(a - 4) (a + 1) = 0
⇒ a = 4 or -1.
Thus, required equation of straight line is
(y - 3) = `((4 - 3)/(5 - 4))(x - 4)`
y - 3 = `(1/1)(x - 4)`
x - y - 1 = 0
or
(y - 3) = `((-1 - 3)/(5 + 1))(x + 1)`
(y - 3) = `(-4/6)(x + 1)`
y - 3 = `(-2)/(3)(x + 1)`
3y - 9 - 2x - 2
2x + 3y - 7 = 0.
APPEARS IN
RELATED QUESTIONS
A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
1) Find the coordinates of the centroid G of the triangle
2) Find the equation of the line through G and parallel to AC
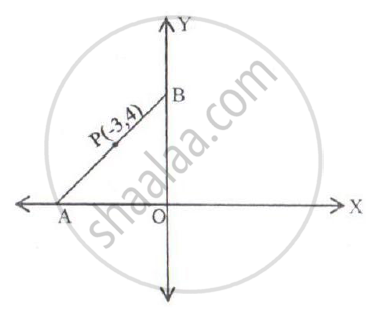
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
The equation of a line 3x + 4y − 7 = 0. Find
1) The slope of the line.
2) The equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
Find the equation of the line, whose x-intercept = −8 and y-intercept = −4
The line 5x + 3y = 25 divides the join of (b,4) and (5, 8) in the ratio of 1 : 3. Find the value of b.
Find the value of a line parallel to the following line:
`(3"y")/4 + (5"y")/2 = 7`
Find the equation of a line whose slope and y-intercept are m = `2/3`, c = -2
Find the equation of a line passing through (-5,-1) and perpendicular to the 3x + y = 9
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
