Advertisements
Advertisements
Question
Find the equation of a line passing through (-5,-1) and perpendicular to the 3x + y = 9
Solution
3x + y = 9
y = -3x + 9
m = -3
Slope of required line = `1/3`
Equation of line is, `("y" - "y"_1)/("x" - "x"_1)` = m
`("y" + 1)/("x" + 5) = 1/3`
⇒ x + 5 = 3y + 3
⇒ x - 3y + 2 = 0
APPEARS IN
RELATED QUESTIONS
Does the line 3x − 5y = 6 bisect the join of (5, −2) and (−1, 2)?
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
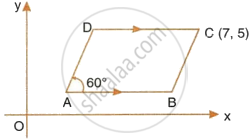
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
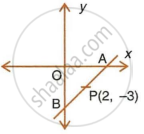
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
Find the equation of a line passing through the intersection of x + 3y = 6 and 2x - 3y = 12 and parallel to the line 5x + 2y = 10
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
