Advertisements
Advertisements
Question
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
Solution
The line 2x + 5y + 12 = 0 passes through (4,m)
(4,m) will satisfy the equation of line
2(4) + 5(m) + 12 = 0
8 + 5m + 12 = 0
5m + 20 = 0
m = `(-20)/5`
`therefore` m = -4
APPEARS IN
RELATED QUESTIONS
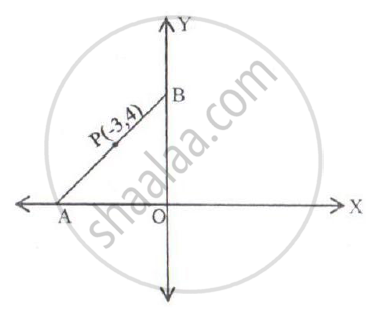
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the equation of a line, through the centroid and parallel to AB.
Find if the following points lie on the given line or not:
(7, -2) on the line 5x + 7y = 11
Find the equation of a line whose slope and y-intercept are m = `(-1)/2`, c = 5
PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
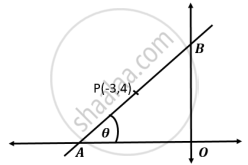
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
