Advertisements
Advertisements
Question
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
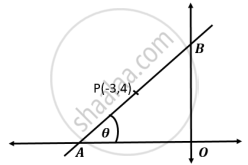
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
Solution
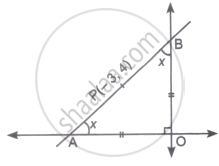
OA = OB
Given, Isosceles Δ so, ∠BAO = ∠ABO = x (let)
∠BAO + ∠ABO + ∠AOB = 180° ...(∵ sum of three angles of a triangle is 180°)
⇒ x + x + 90° = 180°
⇒ 2x = 90°
⇒ x = 45°
∴ ∠BAO = 45° = 𝜃
(a) Slope of AB = tan 45° = 1
Inclination (𝜃) = 45°
(b) AB has slope = 1 and passes through P (-3, 4)
∴ Equation of the line AB is
⇒ y - y1 = m(x - x1)
⇒ y - 4 = 1(x + 3)
⇒ y = x + 3 + 4
y = x + 7
⇒ x - y + 7 = 0
APPEARS IN
RELATED QUESTIONS
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 -4x <= 7 1/2`, x ∈ 1
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the equation of a line passing through (2,9) and parallel to the line 3x + 4y = 11
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
In the adjoining figure, write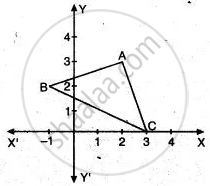
(i) The coordinates of A, B and C.
(ii) The equation of the line through A and | | to BC.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
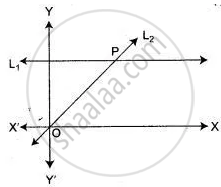
Given equation of line L1 is y = 4.
(i) Write the slope of line, if L2 is the bisector of angle O.
(ii) Write the coordinates of point P.
(iii) Find the equation of L2