Advertisements
Advertisements
Question
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
Solution
Since line is parallel to
3x + 5y + 15 = 0
5y = -3x - 15
y = `(-3)/(5) x - 3`
∴ m1 = `(-3)/(5)`
m1 = m2 ...(∵ lines are parallel)
∴ m2 = `(-3)/(5)`
and passing point = (0, 4)
Equation of line
y - y1 = m(x - x1)
⇒ y - 4 = `(-3)/(5)(x - 0)`
⇒ 5y - 20 = -3x
⇒ 3x + 5y = 20.
APPEARS IN
RELATED QUESTIONS
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(–5, 0)
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x – y = 4.
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.
Find the equation of a line whose slope and y-intercept are m = 2, c = -5
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line passing through (3,7) and making an angle of 60° with the negative direction of the x-axis.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
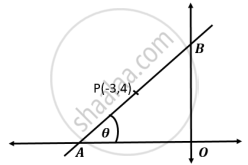
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
