Advertisements
Advertisements
Question
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
Solution
Given, y-intercept = c = −1 and inclination = 45°.
Slope = m = tan 45° = 1
Substituting the values of c and m in the equation y = mx + c, we get,
y = x – 1, which is the required equation.
APPEARS IN
RELATED QUESTIONS
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(1, 3)
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(5, 5)
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(2, –1.5)
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the equation of PQ;
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
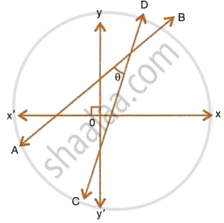
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
Find the value of m if the line 2x + 5y + 12 = 0 passes through the point
( 4,m ).
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.
