Advertisements
Advertisements
Question
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(5, 5)
Solution
The given line is x − 2y + 5 = 0.
Substituting x = 5 and y = 5 in the given equation, we have:
L.H.S. = 5 − 2 × 5 + 5
= 5 − 10 + 5
= 10 − 10
= 0 = R.H.S.
Thus, the point (5, 5) lies on the given line.
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a triangle ABC, `M' is a point on AB such that AM: MB = 1: 2. Find the coordinates of 'M'. Hence find the equation of the line passing through the points C and M
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(1, 3)
Find, if point (-2,-1.5) lie on the line x – 2y + 5 = 0
Find the equation of the line passing through : (−1, −4) and (3, 0)
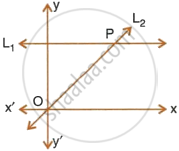
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
Find the equation of a line whose slope and y-intercept are m = `(-6)/5`, c = 3
Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
Find a general equation of a line which passes through:
(i) (0, -5) and (3, 0) (ii) (2, 3) and (-1, 2).
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
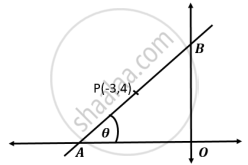
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
