Advertisements
Advertisements
Question
Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
Solution
We have
Slope of the line m = 1
and Y-intercept, c = 5 units
The equation of line is given by
y = mx + c
i.e., y = 1.x + 5
⇒ y = x + 5
or x - y + 5 = 0.
APPEARS IN
RELATED QUESTIONS
State, true or false :
The line `x/ 2 + y/3 = 0` passes through the point (2, 3).
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
Find the equation of the line passing through : (0, 1) and (1, 2)
Find the equation of the line, whose x-intercept = 5 and y-intercept = 3
Find the equations of the line through (1, 3) and making an intercept of 5 on the y-axis.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
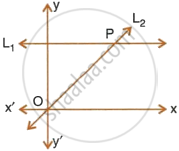
Given equation of line L1 is y = 4.
- Write the slope of line L2 if L2 is the bisector of angle O.
- Write the co-ordinates of point P.
- Find the equation of L2.
Find the inclination of a line whose gradient is 1.4281
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
