Advertisements
Advertisements
Question
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
Solution
Given, the point (−3, 2) lies on the line ax + 3y + 6 = 0.
Substituting x = −3 and y = 2 in the given equation, we have:
a(−3) + 3(2) + 6 = 0
−3a + 12 = 0
3a = 12
a = 4
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
The line x – 6y + 11 = 0 bisects the join of (8, −1) and (0, k). Find the value of k.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
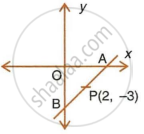
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
The line 7x - 8y = 4 divides join of (-8,-4) and (6,k) in the ratio of 2 : 5. Find the value of k.
Find the inclination of a line whose gradient is 0.4663
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
Find the equation of a line passing through the intersection of x + 3y = 6 and 2x - 3y = 12 and parallel to the line 5x + 2y = 10
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
