Advertisements
Advertisements
Question
The line y = mx + 8 contains the point (−4, 4), calculate the value of m.
Solution
Given, the line y = mx + 8 contains the point (−4, 4).
Substituting x = −4 and y = 4 in the given equation, we have:
4 = −4m + 8
4m = 4 = m = 1
APPEARS IN
RELATED QUESTIONS
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
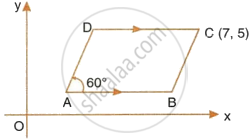
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
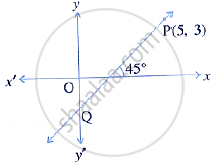
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
Find if the following points lie on the given line or not:
(7, -2) on the line 5x + 7y = 11
The line y = 6- `(3"x")/2` passes through the point (r,3). Find the value of r.
Find the inclination of a line whose gradient is 1.4281
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
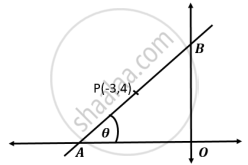
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
