Advertisements
Advertisements
Question
The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?
Solution
Given, the point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3.
Co-ordinates of the point P are
`((2 xx (-3) + 3 xx 2)/(2 + 3),(2 xx 6 + 3 xx 1)/(2 + 3))`
= `((-6 + 6)/(5), (12 + 3)/(5))`
= `(0/5, 15/5)`
= (0, 3)
Substituting x = 0 and y = 3 in the given equation, we have:
L.H.S. = 0 − 5(3) + 15
= −15 + 15
= 0 = R.H.S.
Hence, the point P lies on the line x − 5y + 15 = 0.
APPEARS IN
RELATED QUESTIONS
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
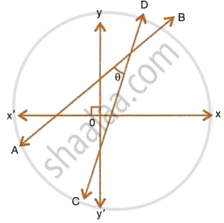
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
The line segment formed by the points (3, 7) and (-7, z) is bisected by the line 3x + 4y =18. Find the value of z.
Find the value of a line parallel to the following line:
`(2"x")/5 + "y"/3` = 2
