Advertisements
Advertisements
Question
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Solution
To prove given lines
2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent, we have to prove that
∴ They will pass through the same point
Now 2x + 5y = 1 ...(i)
x – 3y = 6 ...(ii)
Multiply (i) by 3 and (ii) by 5, we get:
6x + 15y = 3
5x – 15y = 30
On Adding we get:
11x = 33
`\implies x = 33/11 = 3`
From (ii), we have
x – 3y = 6
`\implies` 3 – 3y = 6
`\implies` –3y = 6 – 3 = 3
`\implies y = 3/(-3) = -1`
∴ Point of intersection of first two lines is (3, –1)
Substituting the values in third line
x + 5y + 2 = 0
L.H.S. = x + 5y + 2
= 3 + 5(–1) + 2
= 3 – 5 + 2
= 5 – 5
= 0 = R.H.S.
Hence the given three lines are concurrent.
APPEARS IN
RELATED QUESTIONS
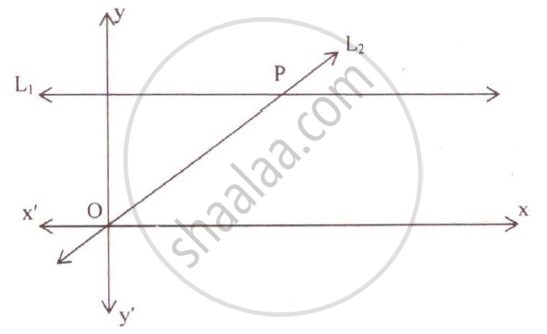
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
The line y = 3x – 2 bisects the join of (a, 3) and (2, −5), find the value of a.
The co-ordinates of two points A and B are (-3, 4) and (2, -1) Find: the co-ordinates of the point where the line AB intersects the y-axis.
Find the equation of the line, whose x-intercept = −4 and y-intercept = 6
Find the value of a line parallel to the following line:
`"x"/4 +"y"/3` = 1
X(4,9), Y(-5,4) and Z(7,-4) are the vertices of a triangle. Find the equation of the altitude of the triangle through X.
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
A and B are two points on the x-axis and y-axis respectively.

- Write down the coordinates of A and B.
- P is a point on AB such that AP : PB = 1 : 1.
Using section formula find the coordinates of point P. - Find the equation of a line passing through P and perpendicular to AB.
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
