Advertisements
Advertisements
Question
X(4,9), Y(-5,4) and Z(7,-4) are the vertices of a triangle. Find the equation of the altitude of the triangle through X.
Solution
The altitude through X is perpendicular tp YZ.
Slope of YZ = `(-4 - 4)/(7 + 5) = (-2)/3`
⇒ m = Slope of YZ = `(-2)/3`
Slope line perpendicular to YZ will be `(-1)/"m" = 3/2`
This line passes through X(4,9)
Using the point slope Formulae,
y - y1 = m(x - x1)
y - 9 = `3/2`(x - 4)
⇒ 2y - 18 = 3x - 12
⇒ 2y = 3x + 6
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the equation of PQ;
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
Find the value of a if the line 4 x = 11 - 3y passes through the point (a, 5)
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
Find the equation of a line passing through (-5,-1) and perpendicular to the 3x + y = 9
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
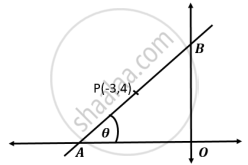
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
