Advertisements
Advertisements
Question
Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.
Solution
Let AB and CD be two equally inclined lines.
For line AB:
Slope = m = tan 45° = 1
(x1, y1) = (−2, 0)
Equation of the line AB is:
y − y1 = m(x − x1)
y − 0 = 1(x + 2)
y = x + 2
For line CD:
Slope = m = tan (−45°) = −1
(x1, y1) = (−2, 0)
Equation of the line CD is:
y − y1 = m(x − x1)
y − 0 = −1(x + 2)
y = −x − 2
x + y + 2 = 0
APPEARS IN
RELATED QUESTIONS
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
Find the inclination of a line whose gradient is 1.4281
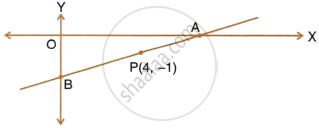
A line AB meets X-axis at A and Y-axis at B. P(4, –1) divides AB in the ration 1 : 2.
- Find the co-ordinates of A and B.
- Find the equation of the line through P and perpendicular to AB.
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
