Advertisements
Advertisements
Question
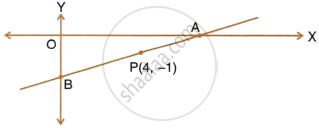
A line AB meets X-axis at A and Y-axis at B. P(4, –1) divides AB in the ration 1 : 2.
- Find the co-ordinates of A and B.
- Find the equation of the line through P and perpendicular to AB.
Solution
i. Since A lies on the X-axis, let the co-ordinates of A be (x, 0).
Since B lies on the Y-axis, let the co-ordinates of B be (0, y).
Let m = 1 and n = 2
Using section formula,
Coordinates of P = `((1(0) + 2(x))/(1 + 2), (1y + 2(0))/(1 + 2))`
`=> (4, -1) = ((2x)/3, y/3)`
`=> (2x)/3 = 4` and `y/3 = -1`
`=>` x = 6 and y = –3
So, the co-ordinates of A are (6, 0) and that of B are (0, –3).
ii. Slope of AB = `(-3 - 0)/(0 - 6) = (-3)/(-6) = 1/2`
`=>` Slope of line perpendicular to AB = m = –2
P = (4, –1)
Thus, the required equation is
y – y1 = m(x – x1)
`=>` y – (–1) = –2(x – 4)
`=>` y + 1 = –2x + 8
`=>` 2x + y = 7
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
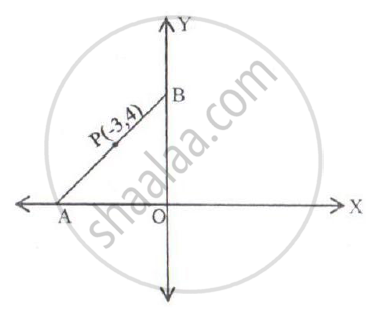
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
Solve the following inequation and represent the solution set on the number line 2x – 5 <= 5x + 4 < 11, where x ∈ I
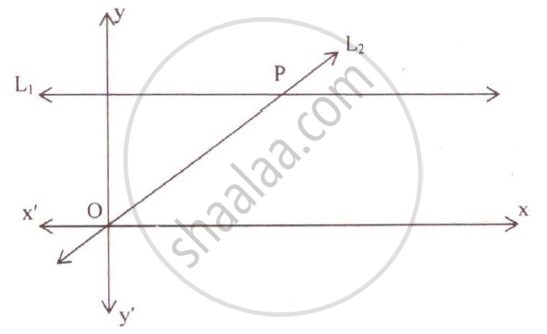
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.
Find the inclination of a line whose gradient is 0.4663
ABCD is a square. The cooordinates of B and D are (-3, 7) and (5, -1) respectively. Find the equation of AC.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
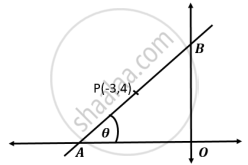
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
