Selina solutions for Mathematics [English] Class 10 ICSE chapter 14 - Equation of a Line [Latest edition]

Find, which of the following points lie on the line x – 2y + 5 = 0 :

(1, 3)

Find, which of the following points lie on the line x – 2y + 5 = 0 :

(0, 5)

Find, which of the following points lie on the line x – 2y + 5 = 0 :

(–5, 0)

Find, which of the following points lie on the line x – 2y + 5 = 0 :

(5, 5)

Find, which of the following points lie on the line x – 2y + 5 = 0 :

(2, –1.5)

Find, if point (-2,-1.5) lie on the line x – 2y + 5 = 0

State, true or false :

The line `x/ 2 + y/3 = 0` passes through the point (2, 3).

State, true or false :

The line `x/2 + y/3 = 0` passes through the point (4, −6).

State, true or false :

The point (8, 7) lies on the line y – 7 = 0

State, true or false :

The point (–3, 0) lies on the line x + 3 = 0

State, true or false :

If the point (2, a) lies on the line 2x – y = 3, then a = 5.

The line given by the equation `2x - y/3 = 7` passes through the point (k, 6); calculate the value of k.

For what value of k will the point (3, −k) lie on the line 9x + 4y = 3?

The line `(3x)/5 - (2y)/3 + 1 = 0` contains the point (m, 2m – 1); calculate the value of m.

Does the line 3x − 5y = 6 bisect the join of (5, −2) and (−1, 2)?

The line y = 3x – 2 bisects the join of (a, 3) and (2, −5), find the value of a.

The line x – 6y + 11 = 0 bisects the join of (8, −1) and (0, k). Find the value of k.

The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.

The line y = mx + 8 contains the point (−4, 4), calculate the value of m.

The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?

The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?

Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.

Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.

Find the slope of the line whose inclination is 0°

Find the slope of the line whose inclination is 30°

Find the slope of the line whose inclination is 72° 30'

Find the slope of the line whose inclination is 46°

Find the inclination of the line whose slope is 0

Find the inclination of the line whose slope is `sqrt(3)`

Find the inclination of the line whose slope is 0.7646

Find the inclination of the line whose slope is 1.0875

Find the slope of the line passing through the following pairs of points:

(−2, −3) and (1, 2)

Find the slope of the line passing through the following pairs of points:

(−4, 0) and origin

Find the slope of the line passing through the following pairs of points:

(a, −b) and (b, −a)

Find the slope of the line parallel to AB if : A = (−2, 4) and B = (0, 6)

Find the slope of the line parallel to AB if : A = (0, −3) and B = (−2, 5)

Find the slope of the line perpendicular to AB if : A = (0, −5) and B = (−2, 4)

Find the slope of the line perpendicular to AB if : A = (3, −2) and B = (−1, 2)

The line passing through (0, 2) and (−3, −1) is parallel to the line passing through (−1, 5) and (4, a). Find a.

The line passing through (−4, −2) and (2, −3) is perpendicular to the line passing through (a, 5) and (2, −1). Find a.

Without using the distance formula, show that the points A(4, −2), B(−4, 4) and C(10, 6) are the vertices of a right-angled triangle.

Without using the distance formula, show that the points A(4, 5), B(1, 2), C(4, 3) and D(7, 6) are the vertices of a parallelogram.

(−2, 4), (4, 8), (10, 7) and (11, –5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.

Show that the points P(a, b + c), Q(b, c + a) and R(c, a + b) are collinear.

Find x, if the slope of the line joining (x, 2) and (8, −11) is `−3/4`.

The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.

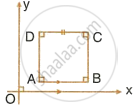
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides. Also, find: 

1. the slope of the diagonal AC.
2. the slope of the diagonal BD.

A(5, 4), B(−3, −2) and C(1, −8) are the vertices of a triangle ABC. Find:

1. the slope of the altitude of AB,
2. the slope of the median AD and
3. the slope of the line parallel to AC.

The slope of the side BC of a rectangle ABCD is `2/3`. Find:

1. the slope of the side AB.
2. the slope of the side AD.

Find the slope and the inclination of the line AB if : A = (−3, −2) and B = (1, 2)

Find the slope and the inclination of the line AB if : A = `(0, - sqrt(3))` and B = (3, 0)

Find the slope and the inclination of the line AB if : A = `(-1, 2sqrt(3))` and B = `(-2, sqrt(3))`

The points (−3, 2), (2, −1) and (a, 4) are collinear. Find a.

The points (K, 3), (2, −4) and (−K + 1, −2) are collinear. Find K.

Plot the points A(1, 1), B(4, 7) and C(4, 10) on a graph paper. Connect A and B and also A and C.

Which segment appears to have the steeper slope, AB or AC?

Justify your conclusion by calculating the slopes of AB and AC.

Find the value(s) of k so that PQ will be parallel to RS. Given : P(2, 4), Q(3, 6), R(8, 1) and S(10, k)

Find the value(s) of k so that PQ will be parallel to RS. Given : P(3, −1), Q(7, 11), R(−1, −1) and S(1, k)

Find the value(s) of k so that PQ will be parallel to RS. Given : P(5, −1), Q(6, 11), R(6, −4k) and S(7, k²)

Find the equation of a line whose : y-intercept = 2 and slope = 3

Find the equation of a line whose : y-intercept = −1 and inclination = 45°

Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).

Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.

Find the equation of the line passing through : (0, 1) and (1, 2)

Find the equation of the line passing through : (−1, −4) and (3, 0)

The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively. Find:

1. the gradient of PQ;
2. the equation of PQ;
3. the co-ordinates of the point where PQ intersects the x-axis.

The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the equation of PQ; 

The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.

The co-ordinates of two points A and B are (–3, 4) and (2, –1). Find:

1. the equation of AB;
2. the co-ordinates of the point where the line AB intersects the y-axis.

The co-ordinates of two points A and B are (-3, 4) and (2, -1) Find: the co-ordinates of the point where the line AB intersects the y-axis.

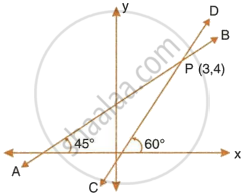
The figure given alongside shows two straight lines AB and CD intersecting each other at point P(3, 4). Find the equations of AB and CD.

In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.

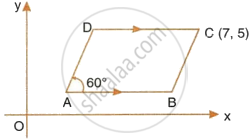
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.

Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x – y = 4.

In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.

A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.

Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).

Find the equation of the line, whose x-intercept = 5 and y-intercept = 3

Find the equation of the line, whose x-intercept = −4 and y-intercept = 6

Find the equation of the line, whose x-intercept = −8 and y-intercept = −4

Find the equation of the line whose slope is `-5/6` and x-intercept is 6.

Find the equation of the line with x-intercept 5 and a point on it (–3, 2).

Find the equations of the line through (1, 3) and making an intercept of 5 on the y-axis.

Find the equations of the lines passing through point (–2, 0) and equally inclined to the co-ordinate axes.

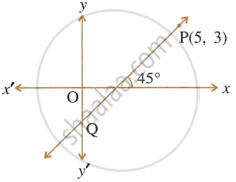
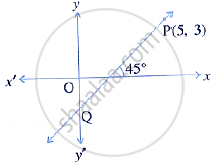
The line through P(5, 3) intersects y-axis at Q.

1. Write the slope of the line.
2. Write the equation of the line.
3. Find the co-ordinates of Q.

The line through P (5, 3) intersects y-axis at Q.
write the equation of the line

The line through P (5, 3) intersects y-axis at Q. 

Find the co-ordinates of Q.

Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.

A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.

A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the equation of a line, through the centroid and parallel to AB.

A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.

Find the slope and y-intercept of the line:

 y = 4

Find the slope and y-intercept of the line:

ax – by = 0

Find the slope and y-intercept of the line:

3x – 4y = 5

The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.

Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?

Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?

Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?

Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.

Find the slope of the line which is parallel to x + 2y + 3 = 0

Find the slope of the line which is parallel to `x/2 - y/3 -1 = 0 `

Find the slope of the line which is perpendicular to `x - y/2 + 3 = 0`

Find the slope of the line which is perpendicular to `x/3 - 2y = 4`

Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.

Lines mx + 3y + 7 = 0 and 5x – ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.

Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3y = 4 are perpendicular to each other.

The equation of a line AB is 2x – 2y + 3 = 0.

1. Find the slope of the line AB.
2. Calculate the angle that the line AB makes with the positive direction of the x-axis.

The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.

If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.

The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.

Find the equation of the line passing through (−5, 7) and parallel to x-axis

Find the equation of the line passing through (−5, 7) and parallel to y-axis

Find the equation of the line passing through (5, –3) and parallel to x – 3y = 4.

Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).

Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.

Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).

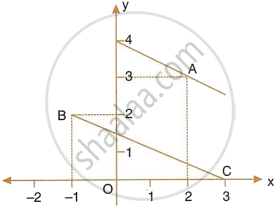
In the following diagram, write down:

1. the co-ordinates of the points A, B and C.
2. the equation of the line through A and parallel to BC.

B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.

A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.

A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the median of the triangle through A.

A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the altitude of the triangle through B.

A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the line through C and parallel to AB.

1. Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
2. AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.

The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.

The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :

1. the equation of the line AP.
2. the co-ordinates of P.

The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.

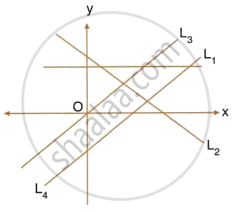
Match the equations A, B, C and D with the lines L₁, L₂, L₃ and L₄, whose graphs are roughly drawn in the given diagram.

A ≡ y = 2x; 

B ≡ y – 2x + 2 = 0;

C ≡ 3x + 2y = 6;

 D ≡ y = 2

Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.

Point P divides the line segment joining the points A(8, 0) and B(16, –8) in the ratio 3 : 5. Find its co-ordinates of point P. Also, find the equation of the line through P and parallel to 3x + 5y = 7.

The line segment joining the points A(3, −4) and B(−2, 1) is divided in the ratio 1 : 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.

A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.

Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other.

A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects the co-ordinate axes at points A and B. M is the mid-point of the segment AB. Find:

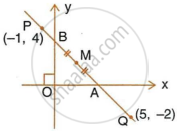
1. The equation of the line.
2. The co-ordinates of A and B.
3. The co-ordinates of M.

(1, 5) and (–3, –1) are the co-ordinates of vertices A and C respectively of rhombus ABCD. Find the equations of the diagonals AC and BD.

Show that A(3, 2), B(6, −2) and C(2, −5) can be the vertices of a square.

1. Find the co-ordinates of its fourth vertex D, if ABCD is a square.
2. Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.

A line through origin meets the line x = 3y + 2 at right angles at point X. Find the co-ordinates of X.

A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.

Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.

Find the equation of the line which is perpendicular to the line `x/a - y/b = 1` at the point where this line meets y-axis.

O(0, 0), A(3, 5) and B(−5, −3) are the vertices of triangle OAB. Find the equation of median of triangle OAB through vertex O.

O(0, 0), A(3, 5) and B(−5, −3) are the vertices of triangle OAB. Find the equation of altitude of triangle OAB through vertex B.

Determine whether the line through points (–2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.

Does line 3x = y + 1 bisect the line segment joining the two given points?

Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).

Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:

1. perpendicular to the line 2x – y + 7 = 0
2. parallel to it.

The vertices of a triangle ABC are A(0, 5), B(−1, −2) and C(11, 7). Write down the equation of BC. Find:

1. the equation of line through A and perpendicular to BC.
2. the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.

From the given figure, find:

1. the co-ordinates of A, B and C.
2. the equation of the line through A and parallel to BC.

P(3, 4), Q(7, –2) and R(–2, –1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R.

A(8, −6), B(−4, 2) and C(0, −10) are vertices of a triangle ABC. If P is the mid-point of AB and Q is the mid-point of AC, use co-ordinate geometry to show that PQ is parallel to BC. Give a special name to quadrilateral PBCQ.

A line AB meets the x-axis at point A and y-axis at point B. The point P(−4, −2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:

1. the co-ordinates of A and B.
2. equation of line through P and perpendicular to AB.

A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.

Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.

The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.

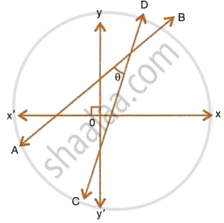
Write down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.

The ordinate of a point lying on the line joining the points (6, 4) and (7, –5) is –23. Find the coordinates of that point.

Point A and B have co-ordinates (7, −3) and (1, 9) respectively. Find:

1. the slope of AB.
2. the equation of perpendicular bisector of the line segment AB.
3. the value of ‘p’ of (−2, p) lies on it.

A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the

1. co-ordinates of A and B
2. slope of line AB
3. equation of line AB.

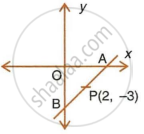
The equation of a line is 3x + 4y – 7 = 0. Find:

1. the slope of the line.
2. the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.

ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, −4). Find:

1. co-ordinates of A.
2. equation of diagonal BD.

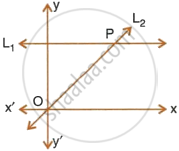
Given equation of line L₁ is y = 4.

1. Write the slope of line L₂ if L₂ is the bisector of angle O.
2. Write the co-ordinates of point P.
3. Find the equation of L₂.

 Find:

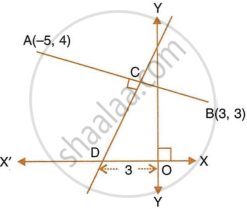
1. equation of AB
2. equation of CD

Find Equation of CD 

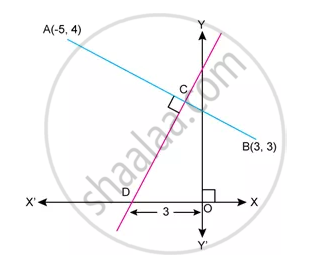
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.

A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find: 

1. the equation of the line. 
2. the co-ordinates of point A and B.
3. the co-ordinates of point M.

In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:

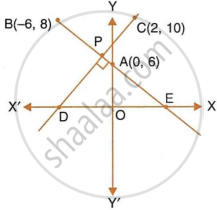
1. equation of line AB.
2. equation of line CD.
3. co-ordinates of points E and D.

A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.

Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.

Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.

Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find: 

1. the co-ordinates of the fourth vertex D. 
2. length of diagonal BD. 
3. equation of side AB of the parallelogram ABCD.

In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively. 

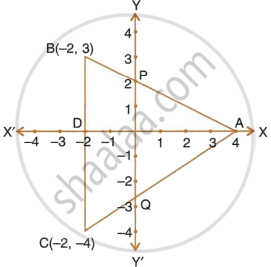
1. Write the co-ordinates of A. 
2. Find the length of AB and AC.
3. Find the radio in which Q divides AC. 
4. Find the equation of the line AC.

The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i). 

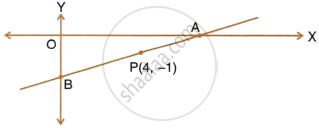
A line AB meets X-axis at A and Y-axis at B. P(4, –1) divides AB in the ration 1 : 2.

1. Find the co-ordinates of A and B.
2. Find the equation of the line through P and perpendicular to AB.