Advertisements
Advertisements
Question
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
Solution
(i) Slope of PQ = `(3 - k)/(1 - 3k - 6)`
`=> 1/2 = (3 - k)/(-3k - 5)`
`=>` -3k - 5 = 2(3 - k)
`=>` -3k - 5 = 6 - 2k
`=>` k = -11
(ii) Substituting in P and Q, we get
P(6, k) = P(6, 11) and Q(1 - 3k,3) = Q(34, 3)
Mid point of PQ = `((6 + 34)/2, (-11 + 3)/2) = (40/2, (-8)/2) = (20, -4)`
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
Find the equation of the line passing through : (0, 1) and (1, 2)
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.
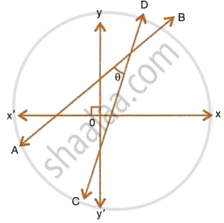
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find if the following points lie on the given line or not:
(7, -2) on the line 5x + 7y = 11
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the line segment joining (2, 3) and (4, 5).
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
