Advertisements
Advertisements
Question
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
Solution
Let the point of intersection of AB and the line 2x-5y+31 =O be the point R ( a,b)
Also, given the line 2x - 5y+31 =0 bisects the line segment AB
AR : RB = 1 : 1
Coordinates of R are,
R (a,b) = R `((-4 + "p")/2 , (5 + 9)/2) = R ((-4 + "p")/2 , 7)`
R (a,b) lies on the line 2x - 5y + 31 = 0
R will satisfy the equation of the line
2`((-4 + "p")/2)` - 5(7) + 31 = 0
⇒ (-4 + p) - 4 = 0
⇒ p = 8
APPEARS IN
RELATED QUESTIONS
If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to one another, find the value of a.
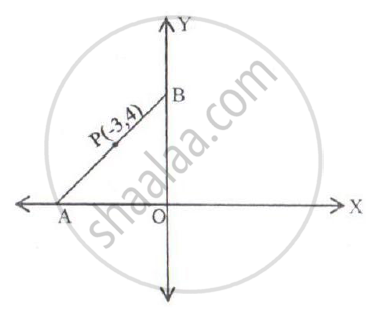
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
State, true or false :
The line `x/ 2 + y/3 = 0` passes through the point (2, 3).
The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
Find the value of a line parallel to the following line:
`(3"y")/4 + (5"y")/2 = 7`
Find the equation of a line whose slope and y-intercept are m = `(-1)/2`, c = 5
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
