Advertisements
Advertisements
प्रश्न
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
उत्तर
Let the point of intersection of AB and the line 2x-5y+31 =O be the point R ( a,b)
Also, given the line 2x - 5y+31 =0 bisects the line segment AB
AR : RB = 1 : 1
Coordinates of R are,
R (a,b) = R `((-4 + "p")/2 , (5 + 9)/2) = R ((-4 + "p")/2 , 7)`
R (a,b) lies on the line 2x - 5y + 31 = 0
R will satisfy the equation of the line
2`((-4 + "p")/2)` - 5(7) + 31 = 0
⇒ (-4 + p) - 4 = 0
⇒ p = 8
APPEARS IN
संबंधित प्रश्न
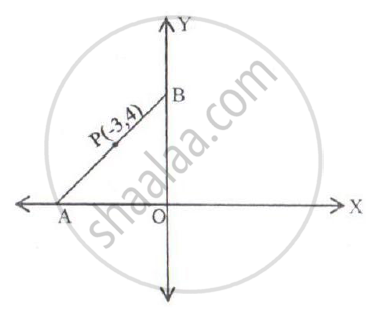
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
State, true or false :
The point (–3, 0) lies on the line x + 3 = 0
State, true or false :
If the point (2, a) lies on the line 2x – y = 3, then a = 5.
The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?
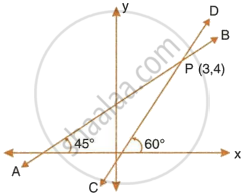
The figure given alongside shows two straight lines AB and CD intersecting each other at point P(3, 4). Find the equations of AB and CD.
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
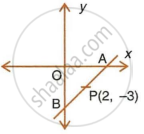
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
The coordinates of two points P and Q are (0,4) and (3,7) respectively. Find
(i) The gradient of PQ
(ii) the equation of PQ
(iii) the coordinates of the point where the line AB intersects the X-axis.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
Which of the following equation represents a line equally inclined to the axes?
