Advertisements
Advertisements
प्रश्न
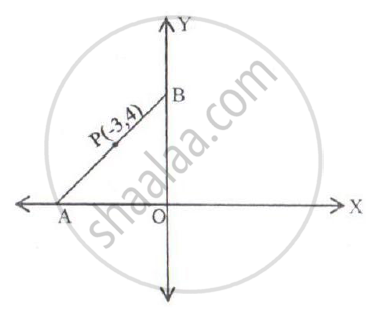
In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
उत्तर
Let the coordinates of A and B be (x, 0) and (0, y) respectively.
Given P divides AB is the ratio 2:3,
Using section formula, we have
`-3 = (2 xx 0 + 3 xx x)/(2 + 3)`
`-3 = "3x"/5`
`-15 = 3x`
x = -5
and
`4 = (2 xx y + 3 xx 0)/(2 + 0)`
`4 = "2y"/5`
20 = 2y
y = 10
Thus, the coordinates of A and B are (–5, 0) and (0, 10) respectively.
APPEARS IN
संबंधित प्रश्न
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
The co-ordinates of two points A and B are (–3, 4) and (2, –1). Find:
- the equation of AB;
- the co-ordinates of the point where the line AB intersects the y-axis.
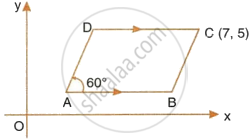
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
The vertices of a triangle ABC are A(0, 5), B(−1, −2) and C(11, 7). Write down the equation of BC. Find:
- the equation of line through A and perpendicular to BC.
- the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.
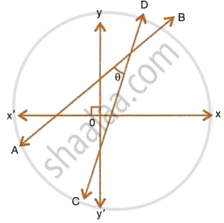
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find if the following points lie on the given line or not:
(5,3) on the line 3x - 5y + 5 = 0
The line 7x - 8y = 4 divides join of (-8,-4) and (6,k) in the ratio of 2 : 5. Find the value of k.
Find the value of a line parallel to the following line:
`"x"/4 +"y"/3` = 1
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
