Advertisements
Advertisements
प्रश्न
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
उत्तर
Equation of median AD
y – y1 = `(y_2 - y_1)/(x_2 - x_1) (x - x_1)`
`\implies` y – (–1) = `(4 - (-1))/(-3 - 1) (x - 1)`
`\implies` y + 1 = `5/-4 (x - 1)`
`\implies` – 4y – 4 = 5x – 5
i.e. 5x + 4y = 1
APPEARS IN
संबंधित प्रश्न
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(5, 5)
State, true or false :
The line `x/ 2 + y/3 = 0` passes through the point (2, 3).
The line given by the equation `2x - y/3 = 7` passes through the point (k, 6); calculate the value of k.
Find the equation of the line, whose x-intercept = −4 and y-intercept = 6
Find the equation of the line with x-intercept 5 and a point on it (–3, 2).
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
P(5,3), Q(-4,7) and R(8,3) are he vertices of a traingles. Find the equation of the median of the traiangle from p.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
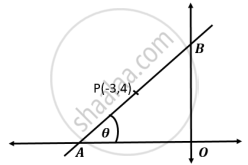
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
A and B are two points on the x-axis and y-axis respectively.

- Write down the coordinates of A and B.
- P is a point on AB such that AP : PB = 1 : 1.
Using section formula find the coordinates of point P. - Find the equation of a line passing through P and perpendicular to AB.
