Question

A and B are two points on the x-axis and y-axis respectively.

1. Write down the coordinates of A and B.
2. P is a point on AB such that AP : PB = 1 : 1.
   Using section formula find the coordinates of point P.
3. Find the equation of a line passing through P and perpendicular to AB.

Answer 1

a. Coordinates of A are (4, 0)

and coordinates of B are (0, 4)

b. AP : PB = 3 : 1

i.e.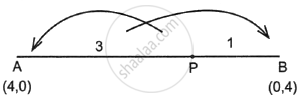

Coordinates of P are

`((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`

= `((3 xx 0 + 1 xx 4)/(3 + 1), (3 xx 4 + 1 xx 0)/(3 + 1))`

= `(4/4, 12/4)`

= (1, 3)

c. Slope of A = `(y_2 - y_1)/(x_2 - x_1)`

= `(4 - 0)/(0 - 4)`

= – 1

∴ Slope of the line perpendicular to AB

m = 1

Equation of line perpendicular to AB and passing through P(1, 3) is

y – y₁ = m(x – x₁)

`\implies` y – 3 = 1(x – 1)

`\implies` y – 3 = x – 1

`\implies` x – y + 2 = 0