Advertisements
Advertisements
प्रश्न
The line 7x - 8y = 4 divides join of (-8,-4) and (6,k) in the ratio of 2 : 5. Find the value of k.
उत्तर
Let the point of intersection of AB and the line 7x-8y=4, be the point P (a,b)
Also, given the line 7x-8y = 4 divides the line segment AB in the ratio 2 : 5.
i.e. AP: PB = 2: 5
Coordinates of P are,
P (a,b) = P `((12 - 40)/7 , (2"k" - 20)/7) = "P" (-4, (2"k" - 20)/7)`
P (a,b) lies on the line 7x - 8y = 4,
P will satisfy the equation of the line
7(-4) - `((2"k" - 20)/7)` = 4
-8 `((2"k" - 20)/7)` = 32
2k - 20 = -28
2k = -8
k = -4
APPEARS IN
संबंधित प्रश्न
Find, if point (-2,-1.5) lie on the line x – 2y + 5 = 0
The line y = mx + 8 contains the point (−4, 4), calculate the value of m.
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
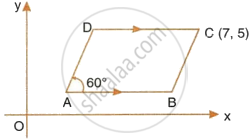
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
The line 5x + 3y = 25 divides the join of (b,4) and (5, 8) in the ratio of 1 : 3. Find the value of b.
Find the equation of a line whose slope and y-intercept are m = `2/3`, c = -2
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
