Advertisements
Advertisements
Question
The line segment formed by the points (3, 7) and (-7, z) is bisected by the line 3x + 4y =18. Find the value of z.
Solution
Let the point of intersection of AB and the line 3x + 4y = 18 be the point P (a,b)
Also, given the line 3x + 4y= 18 bisects the line segment AB
AP : PB = 1 : 1
Coornating of P are,
P(a,b) = P `((3 -7)/2 , (7 + "z")/2) = "P"(-2 (7 + "z")/2)`
P (a,b) lies on the line 3x + 4y = 18,
P will satisfythe equation of the line
3(-2) + 4 `((7 +"z")/2)`= 18
⇒ 14 + 2z = 24
⇒ 2z = 10
⇒ z = 5
APPEARS IN
RELATED QUESTIONS
A(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
1) Find the coordinates of the centroid G of the triangle
2) Find the equation of the line through G and parallel to AC
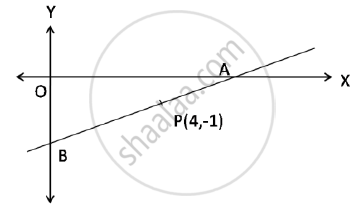
A line AB meets X – axis at A and Y –axis at B. P (4, -1) divides AB in the ratio 1 : 2.
1) Find the coordinates of A and B.
2) Find the equation of the line through P and perpendicular to AB.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(–5, 0)
The line x – 6y + 11 = 0 bisects the join of (8, −1) and (0, k). Find the value of k.
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
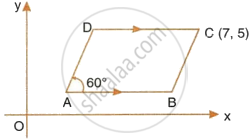
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the co-ordinates of the centroid of triangle ABC.
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the value of a line parallel to the following line:
`"x"/4 +"y"/3` = 1
