Advertisements
Advertisements
Question
The line 5x - 3y +1 = 0 divides the join of (2,m) and (7,9) in the ratio 2: 3. Find the value of m.
Solution
Let the point of intersection of PQ and 5x - 3y + 1 = 0 be the point R( a, b ).
Also given the line 5x -3y+ 1=0 divides the line segment PQ in the ratio 2:3,
i.e. PR : PQ = 2 : 5
Coordinates of R are,
R (a,b) = R `((14 + 6)/5 , (18 + 3"m")/5) = "R" (4, (18 + 3"m")/5)`
R (a,b) lies on the line 5x - 3y + 1 = 0
R will satisfy the equation of the line
5(4) - 3 `((18 = 3"m")/5)` + 1 = 0
⇒ -3 `((18 + 3"m")/5)` = -21
⇒ 18 + 3m = 35
⇒ 3m = 17
⇒ m = `17/3`
APPEARS IN
RELATED QUESTIONS
The line y = 3x – 2 bisects the join of (a, 3) and (2, −5), find the value of a.
The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
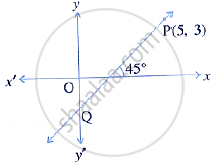
Find the equation of a line whose slope and y-intercept are m = `(-1)/2`, c = 5
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
