Advertisements
Advertisements
Question
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Solution
m = tan 30°
=`1/sqrt 3`
Equation of line is given by,
`("y" - "y"_1)/("x" - "x"_1)` = m
⇒ `("y" - 5)/("x" - 2) = 1/sqrt3`
⇒ x - 2 = `sqrt3"y" - 5sqrt3`
⇒ x - `sqrt3"y" - 2 + 5sqrt3 = 0`
⇒ `sqrt3"y" = "x" - 2 + 5sqrt3`
APPEARS IN
RELATED QUESTIONS
Find the equation of the line passing through : (−1, −4) and (3, 0)
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
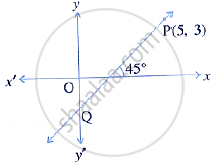
The line through P (5, 3) intersects y-axis at Q.
write the equation of the line
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
P is a point on the line segment AB dividing it in the ratio 2 : 3. If the coordinates of A and Bare (-2,3) and (8,8), find if Plies on the line 7x - 2y =4.
Find the equation of a line passing through (3,7) and making an angle of 60° with the negative direction of the x-axis.
ABCD is rhombus. The coordinates of A and C ae (3,7) and (9,15). Find the equation of BD.
Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.
Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the line segment joining (2, 3) and (4, 5).
