Advertisements
Advertisements
Question
ABCD is rhombus. The coordinates of A and C ae (3,7) and (9,15). Find the equation of BD.
Solution
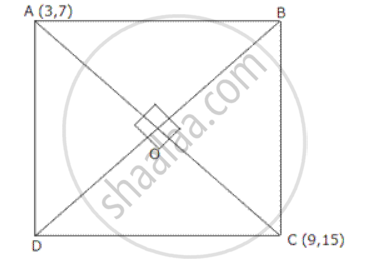
Diagnols of a rhombus bisect each other
`therefore` mid point of BD = mid point of AC
= `"O"((3 + 9)/2 ,(7 + 15)/2)`
= O (6,11)
Slope of AC = `(15 - 7)/(9 - 3) = 8/6 = 4/3`
Slope of BD = `-1/"Slope of AC" = (-3)/4`
Equation of BD is, `("y" - "y"_1)/("x" - "x"_1)` = Slope
`("y" - 4)/("x" - 6) = (-3)/4`
⇒ -3x + 18 = 4y - 44
⇒ x + 4y = 62
APPEARS IN
RELATED QUESTIONS
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 -4x <= 7 1/2`, x ∈ 1
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
State, true or false :
The point (8, 7) lies on the line y – 7 = 0
State, true or false :
The point (–3, 0) lies on the line x + 3 = 0
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the co-ordinates of the point where PQ intersects the x-axis.
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Find the value of a if the line 4 x = 11 - 3y passes through the point (a, 5)
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.
A and B are two points on the x-axis and y-axis respectively.

- Write down the coordinates of A and B.
- P is a point on AB such that AP : PB = 1 : 1.
Using section formula find the coordinates of point P. - Find the equation of a line passing through P and perpendicular to AB.
