Advertisements
Advertisements
प्रश्न
ABCD is rhombus. The coordinates of A and C ae (3,7) and (9,15). Find the equation of BD.
उत्तर
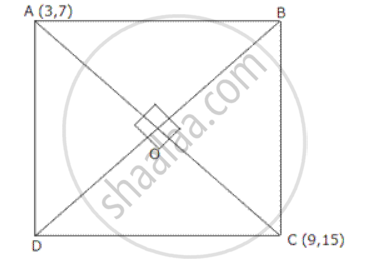
Diagnols of a rhombus bisect each other
`therefore` mid point of BD = mid point of AC
= `"O"((3 + 9)/2 ,(7 + 15)/2)`
= O (6,11)
Slope of AC = `(15 - 7)/(9 - 3) = 8/6 = 4/3`
Slope of BD = `-1/"Slope of AC" = (-3)/4`
Equation of BD is, `("y" - "y"_1)/("x" - "x"_1)` = Slope
`("y" - 4)/("x" - 6) = (-3)/4`
⇒ -3x + 18 = 4y - 44
⇒ x + 4y = 62
APPEARS IN
संबंधित प्रश्न
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 -4x <= 7 1/2`, x ∈ 1
Solve the following inequation and represent the solution set on the number line 2x – 5 <= 5x + 4 < 11, where x ∈ I
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
Find the equation of a line whose slope and y-intercept are m = 2, c = -5
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
Given equation of line L1 is y = 4.
(i) Write the slope of line, if L2 is the bisector of angle O.
(ii) Write the coordinates of point P.
(iii) Find the equation of L2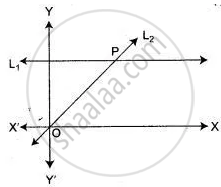
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
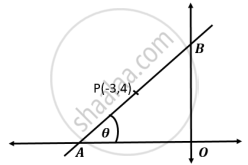
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
