Advertisements
Advertisements
प्रश्न
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
उत्तर
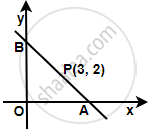
Let the line intersect the x-axis at point A(x, 0) and y-axis at point B(0, y).
Since, P is the mid-point of AB, we have:
`((x + 0)/2, (0 + y)/2) = (3, 2)`
`(x/2, y/2) = (3, 2)`
x = 6, y = 4
Thus, A = (6, 0) and B = (0, 4)
Slope of line AB = `(4 - 0)/(0 - 6) = 4/(-6) = (-2)/3`
Let (x1, y1) = (6, 0)
The required equation of the line AB is given by
y – y1 = m(x – x1)
`y - 0 = (-2)/3 (x - 6)`
3y = −2x + 12
2x + 3y = 12
APPEARS IN
संबंधित प्रश्न
The line given by the equation `2x - y/3 = 7` passes through the point (k, 6); calculate the value of k.
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
The vertices of a triangle ABC are A(0, 5), B(−1, −2) and C(11, 7). Write down the equation of BC. Find:
- the equation of line through A and perpendicular to BC.
- the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
P(5,3), Q(-4,7) and R(8,3) are he vertices of a traingles. Find the equation of the median of the traiangle from p.
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
ABCD is rhombus. The coordinates of A and C ae (3,7) and (9,15). Find the equation of BD.
In the given diagram, OA = OB, ∠OAB = 𝜃 and the line AB passes through point P (-3, 4).
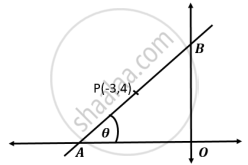
Find:
- Slope and inclination (𝜃) of the line AB
- Equation of the line AB
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
Which of the following equation represents a line equally inclined to the axes?
