Advertisements
Advertisements
प्रश्न
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
उत्तर
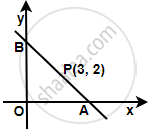
Let the line intersect the x-axis at point A(x, 0) and y-axis at point B(0, y).
Since, P is the mid-point of AB, we have:
`((x + 0)/2, (0 + y)/2) = (3, 2)`
`(x/2, y/2) = (3, 2)`
x = 6, y = 4
Thus, A = (6, 0) and B = (0, 4)
Slope of line AB = `(4 - 0)/(0 - 6) = 4/(-6) = (-2)/3`
Let (x1, y1) = (6, 0)
The required equation of the line AB is given by
y – y1 = m(x – x1)
`y - 0 = (-2)/3 (x - 6)`
3y = −2x + 12
2x + 3y = 12
APPEARS IN
संबंधित प्रश्न
State, true or false :
The line `x/2 + y/3 = 0` passes through the point (4, −6).
The point P divides the join of (2, 1) and (−3, 6) in the ratio 2 : 3. Does P lies on the line x − 5y + 15 = 0?
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
Find the equation of the line passing through : (0, 1) and (1, 2)
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the inclination of a line whose gradient is 5.6713
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
ABCD is a square. The cooordinates of B and D are (-3, 7) and (5, -1) respectively. Find the equation of AC.
