Advertisements
Advertisements
Question
Solve the following inequation and represent the solution set on a number line.
`-8 1/2 < -1/2 -4x <= 7 1/2`, x ∈ 1
Solution
`-81/2 < -1/2-4x<=71/2`, x ∈ I
`=> -17/2 < -1/2 - 4x <= 15/2`, x ∈ I
Take `-17/2 < -1/2 - 4x` `-1/2 - 4x <= 15/2`
`-17/2 + 1/2 < -4x` `-4x <= 15/2 + 1/2`
`-16/2 < -4x` `-4x <= 16/2`
-8 < -4x `-4x <= 8`
2 > x `x >= -2`
Thus, on simplifying, the given inequation reduces to -2 ≤ x 2.
Since x ∈ I, the solution set is { -2, -1, 0, 1}.
The required graph on the number line is as follows:

APPEARS IN
RELATED QUESTIONS
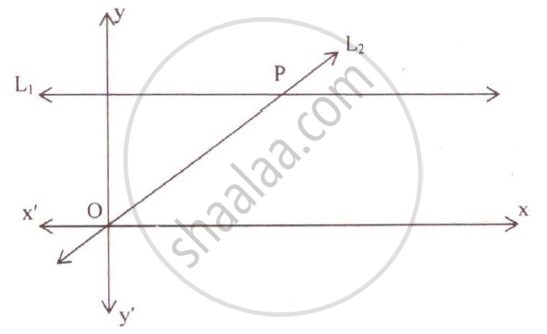
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find:
(i) Slope of BC
(ii) Equation of a line perpendicular to BC and passing through A.
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(– 6, 4). D is the midpoint of BC. Find the equation of the median AD.
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
