Advertisements
Advertisements
Question
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Solution
Let the point on x-axis be P (x,y) which divides the line segment AB in the ratio 1 : 2,
i.e. AP : PB = 1 : 2
Coordinates of P are,
P (x,y) = P `(( 5 + 4)/3 , ( 6 + 6)/3)`
x = 3, y=4
If P (x,y) lies on the line 3x - 4y + 5 =O, then it will satisfy the equation of the line.
LHS = 3 (3) - 4 ( 4)+ 5 = 9 - 9 = 0 = RHS
Yes, the point Plies on the line 3x - 4y + 5 = 0.
APPEARS IN
RELATED QUESTIONS
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
Find the equation of the line, whose x-intercept = 5 and y-intercept = 3
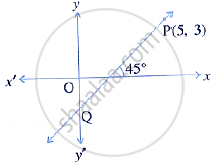
The line through P (5, 3) intersects y-axis at Q.
write the equation of the line
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the equation of a line, through the centroid and parallel to AB.
The slope of aline joining P(6,k) and Q(1 - 3k, 3) is `1/2` Find
(i) k.
(ii) mid-point of PQ, using the value of 'k' found in (i).
Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.
Find the equation of the straight line which has Y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
A and B are two points on the x-axis and y-axis respectively.

- Write down the coordinates of A and B.
- P is a point on AB such that AP : PB = 1 : 1.
Using section formula find the coordinates of point P. - Find the equation of a line passing through P and perpendicular to AB.
