Advertisements
Advertisements
Question
Find the equation of the straight line which has Y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
Solution
Equation of the given line is
3x - 4y + 11 = 0
Slope of this line y = mx + c
4y = 3x + 11
y = `(3)/(4) x + (11)/(4)`
m1 = `(3)/(4)`
Let m2 be the slope of the line which is perpendicular toi the given line then
m1m2 = -1
`(3)/(4)m_2` = -1
⇒ m2 = `-(4)/(3)`.
Also, Y-intercept c = `(4)/(3)`.
Equation of the required line
y = m2x + c
y = `(-4)/(3) x + (4)/(3)`
⇒ 3y = -4x + 4
⇒ 4x + 3y - 4 = 0.
APPEARS IN
RELATED QUESTIONS
The line `(3x)/5 - (2y)/3 + 1 = 0` contains the point (m, 2m – 1); calculate the value of m.
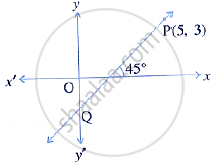
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Determine whether the line through points (–2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.
Does line 3x = y + 1 bisect the line segment joining the two given points?
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
The line 4x + 3y = 11 bisects the join of ( 6,m) and (p,9). Find the value of m.
The line segment formed by two points A (2,3) and B (5, 6) is divided by a point in the ratio 1 : 2. Find, whether the point of intersection lies on the line 3x - 4y + 5 = 0.
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line passing through (8,3) and making an angle of 45° with the positive direction of the y-axis.
ABCD is rhombus. The coordinates of A and C ae (3,7) and (9,15). Find the equation of BD.
Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).
