Advertisements
Advertisements
Question
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
Solution
x - 3y + 5 = 0
⇒ 3y = x + 5
∴ y = `x/(3) + (5)/(3)`
∴ m1 = `(1)/(3)`
Since lines are perpendicular to each other
∴ m1 x m2 = -1
`(1)/(3) xx m_2` = -1
m2 = -1 x 3
m2 = -3
Passing point is (3, -2)
∴ Equation of line
y - y1 = m(x - x1)
⇒ y + 2 = -3(x - 3)
⇒ y + 2 = -3x + 9
⇒ 3x + y + 2 - 9 = 0
⇒ 3x + y =7.
APPEARS IN
RELATED QUESTIONS
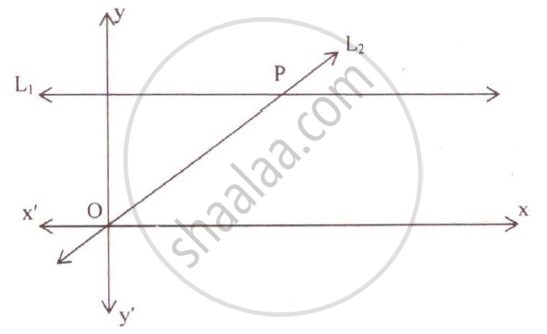
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
State, true or false :
The line `x/ 2 + y/3 = 0` passes through the point (2, 3).
Does the line 3x − 5y = 6 bisect the join of (5, −2) and (−1, 2)?
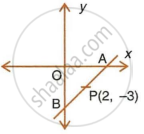
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
The line 2x - 5y + 31 = 0 bisects the join of (-4,5) and (P, 9). Find the value of p.
Find the inclination of a line whose gradient is 5.6713
Find the value of a line parallel to the following line:
x = `"y"/2` - 5
Find the equation of a line whose slope and y-intercept are m = `2/3`, c = -2
