Advertisements
Advertisements
Question
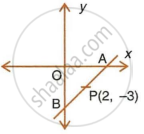
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
Solution
i. Let the co-ordinates be A(x, 0) and B(0, y).
Mid-point of A and B is given by
`((x + 0)/2, (y + 0)/2) = (x/2, y/2)`
`=> (2 ,-3) = (x/2, y/2)`
`=> x/2 = 2` and `y/2 = -3`
`=>` x = 4 and y= −6
∴ A = (4, 0) and B = (0, −6)
ii. Slope of line AB, m = `(y_2 - y_1)/(x_2 -x_1)`
= `(-6 - 0)/(0 - 4)`
= `3/2`
= `1 1/2`
iii. Equation of line AB, using A(4, 0)
y – y1 = m(x – x1)
`y - 0 = 3/2 (x - 4)`
2y = 3x – 12
3x – 2y = 12
APPEARS IN
RELATED QUESTIONS
State, true or false :
If the point (2, a) lies on the line 2x – y = 3, then a = 5.
The line y = 3x – 2 bisects the join of (a, 3) and (2, −5), find the value of a.
The line y = mx + 8 contains the point (−4, 4), calculate the value of m.
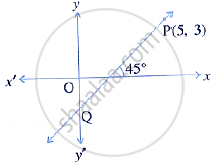
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
The line 7x - 8y = 4 divides join of (-8,-4) and (6,k) in the ratio of 2 : 5. Find the value of k.
Find the equation of a line whose slope and y-intercept are m = `2/3`, c = -2
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
Which of the following equation represents a line equally inclined to the axes?
