Advertisements
Advertisements
प्रश्न
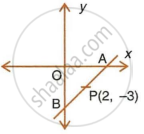
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
उत्तर
i. Let the co-ordinates be A(x, 0) and B(0, y).
Mid-point of A and B is given by
`((x + 0)/2, (y + 0)/2) = (x/2, y/2)`
`=> (2 ,-3) = (x/2, y/2)`
`=> x/2 = 2` and `y/2 = -3`
`=>` x = 4 and y= −6
∴ A = (4, 0) and B = (0, −6)
ii. Slope of line AB, m = `(y_2 - y_1)/(x_2 -x_1)`
= `(-6 - 0)/(0 - 4)`
= `3/2`
= `1 1/2`
iii. Equation of line AB, using A(4, 0)
y – y1 = m(x – x1)
`y - 0 = 3/2 (x - 4)`
2y = 3x – 12
3x – 2y = 12
APPEARS IN
संबंधित प्रश्न
State, true or false :
The line `x/ 2 + y/3 = 0` passes through the point (2, 3).
The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?
Find the point of intersection of the lines 4x + 3y = 1 and 3x − y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
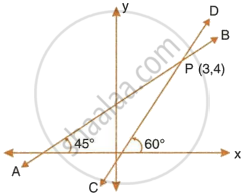
The figure given alongside shows two straight lines AB and CD intersecting each other at point P(3, 4). Find the equations of AB and CD.
In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (–2, 3) and (0, 1) respectively. Find the equation of median through vertex A. Also, find the equation of the line through vertex B and parallel to AC.
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of points P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.
Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
