Advertisements
Advertisements
प्रश्न
The line segment joining the points (5, −4) and (2, 2) is divided by the points Q in the ratio 1 : 2. Does the line x – 2y = 0 contain Q?
उत्तर
Given, the line segment joining the points (5, −4) and (2, 2) is divided by the point Q in the ratio 1 : 2.
Co-ordinates of the point Q are
`((1 xx 2 + 2 xx 5)/(1 + 2),(1 xx 2 + 2 xx (-4))/(1 + 2))`
= `((2 + 10)/3, (2 - 8)/3)`
= `(12/3, (-6)/3)`
= (4, –2)
Substituting x = 4 and y = –2 in the given equation, we have:
L.H.S. = x − 2y
= 4 − 2(−2)
= 4 + 4
= 8 ≠ R.H.S.
Hence, the given line does not contain point Q.
APPEARS IN
संबंधित प्रश्न
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
The line y = mx + 8 contains the point (−4, 4), calculate the value of m.
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
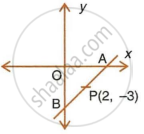
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
The equation of a line is 3x + 4y – 7 = 0. Find:
- the slope of the line.
- the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
Find the value of p if the line 3y = 5x - 7 passes through the point (p,6).
The line y = 6- `(3"x")/2` passes through the point (r,3). Find the value of r.
X(4,9), Y(-5,4) and Z(7,-4) are the vertices of a triangle. Find the equation of the altitude of the triangle through X.
Find the equation of a straight line which cuts an intercept of 5 units on Y-axis and is parallel to the line joining the points (3, – 2) and (1, 4).
Which of the following equation represents a line equally inclined to the axes?
