Advertisements
Advertisements
प्रश्न
Which of the following equation represents a line equally inclined to the axes?
पर्याय
2x – 3y + 7 = 0
x – y = 7
x = 7
y = –7
उत्तर
x – y = 7
Explanation:
A line equally inclined to the x-axis and y-axis means that the line makes an angle of 45° or 135° with the positive x-axis. Such lines have slopes of 1 or –1.
For the line x – y = 7:
- Rearrange to slope-intercept form: y = x – 7
- The slope is 1, indicating the line is inclined at 45° to the positive x-axis, hence equally inclined to both axes.
APPEARS IN
संबंधित प्रश्न
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(2, –1.5)
The line x – 6y + 11 = 0 bisects the join of (8, −1) and (0, k). Find the value of k.
The line segment joining the points A(3, −4) and B(−2, 1) is divided in the ratio 1 : 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.
Find the value of a line parallel to the following line:
x = `"y"/2` - 5
Find the value of a line parallel to the following line:
`(3"y")/4 + (5"y")/2 = 7`
Find the value of a line parallel to the following line:
`(2"x")/5 + "y"/3` = 2
Find the equation of a line passing through (2,9) and parallel to the line 3x + 4y = 11
In the adjoining figure, write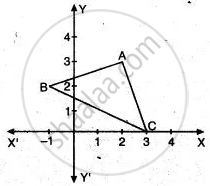
(i) The coordinates of A, B and C.
(ii) The equation of the line through A and | | to BC.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
