Advertisements
Advertisements
प्रश्न
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.
उत्तर
Equation of the line passing through AC is
(y - 3) = `((a - 3)/(5 - a))(x - a)`
As if A, B and C are callinear than B will satisfy it, i.e.,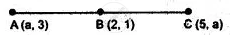
(1 - 3) = `((a - 3)/(5 - a)) (2 - a)`
-2(5 - a) = (a - 3) (2 - a)
-10 + 2a = 2a - 6 - a2 + 3a
a2 - 3a - 4 = 0
a2 - 4a +a - 4 = 0
a(a - 4) + 1 (a - 4) = 0
(a - 4) (a + 1) = 0
⇒ a = 4 or -1.
Thus, required equation of straight line is
(y - 3) = `((4 - 3)/(5 - 4))(x - 4)`
y - 3 = `(1/1)(x - 4)`
x - y - 1 = 0
or
(y - 3) = `((-1 - 3)/(5 + 1))(x + 1)`
(y - 3) = `(-4/6)(x + 1)`
y - 3 = `(-2)/(3)(x + 1)`
3y - 9 - 2x - 2
2x + 3y - 7 = 0.
APPEARS IN
संबंधित प्रश्न
State, true or false :
If the point (2, a) lies on the line 2x – y = 3, then a = 5.
Does the line 3x − 5y = 6 bisect the join of (5, −2) and (−1, 2)?
Find the equation of the line whose slope is `-4/3` and which passes through (−3, 4).
Find the equation of the line, whose x-intercept = −4 and y-intercept = 6
Find the equations of the line through (1, 3) and making an intercept of 5 on the y-axis.
Write down the equation of the line whose gradient is `-2/5` and which passes through point P, where P divides the line segement joining A(4, −8) and B(12, 0) in the ratio 3 : 1.
A(1, 4), B(3, 2) and C(7, 5) are vertices of a triangle ABC. Find the equation of a line, through the centroid and parallel to AB.
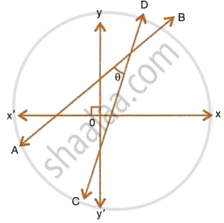
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
The line 4x + 3y = 11 bisects the join of ( 6,m) and (p,9). Find the value of m.
