Advertisements
Advertisements
प्रश्न
Find the equations of the line through (1, 3) and making an intercept of 5 on the y-axis.
उत्तर
Since, y-intercept = 5, so the corresponding point on y-axis is (0, 5).
The line passes through (1, 3).
∴ Slope of the line = `(5 - 3)/(0 - 1) = 2/(-1) = -2`
Required equation of the line is given by:
y − y1 = m(x − x1)
y − 5 = −2(x − 0)
y − 5 = −2x
2x + y = 5
APPEARS IN
संबंधित प्रश्न
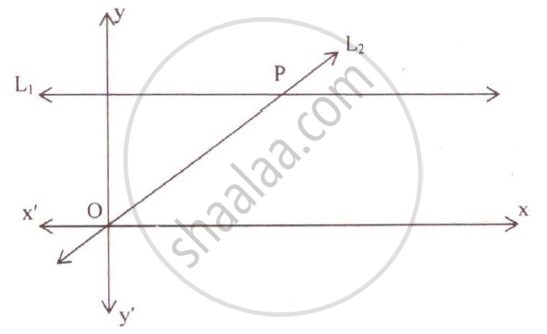
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
State, true or false :
The point (8, 7) lies on the line y – 7 = 0
The point (−3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.
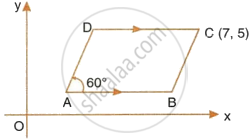
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
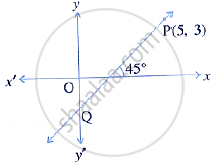
The line through P (5, 3) intersects y-axis at Q.
Find the co-ordinates of Q.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
Find if the following points lie on the given line or not:
(-1, 5) on the line 3x = 2y -15
Find the value of a line parallel to the following line:
x = `"y"/2` - 5
X(4,9), Y(-5,4) and Z(7,-4) are the vertices of a triangle. Find the equation of the altitude of the triangle through X.
Find the equation of a straight line which cuts an intercept of 5 units on Y-axis and is parallel to the line joining the points (3, – 2) and (1, 4).
