Advertisements
Advertisements
प्रश्न
If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.
उत्तर
Let CD be the line mirror with slope m1.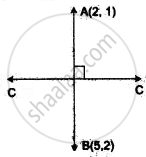
Now the slope of the line joining A(2, 1) and B(5, 2).
m2 = `(2 - 1)/(5 - 2) = (1)/(3)`
Since CD ⊥ AB
So, m1m2 = -1
⇒ `m_1 xx (1)/(3)` = -1
⇒ m1 = -3.
Now mid point of AB = `((2+ 5)/2, (1 + 2)/2) = (7/2, 3/2)`
Equation of the mirror CD,
y = y1 = m(x - x1)
⇒ `y - (3)/(2) = -3(x-7/2)`
⇒ `y - (3)/(2) = -3x + (21)/(2)`
⇒ 2y - 3 = -6x + 21
⇒ 6x + 2y - 3 - 21 = 0
⇒ 6x + 2y - 24 = 0
or 3x + y - 12 = 0.
APPEARS IN
संबंधित प्रश्न
The line y = mx + 8 contains the point (−4, 4), calculate the value of m.
The co-ordinates of two points P and Q are (2, 6) and (−3, 5) respectively Find the equation of PQ;
A(7, −1), B(4, 1) and C(−3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP : CP = 2 : 3.
Write down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.
The equation of a line is 3x + 4y – 7 = 0. Find:
- the slope of the line.
- the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
Find the equation of a line passing through (2,5) and making and angle of 30° with the positive direction of the x-axis.
Find the equation of a line passing through (8,3) and making an angle of 45° with the positive direction of the y-axis.
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
The coordinates of two points P and Q are (0,4) and (3,7) respectively. Find
(i) The gradient of PQ
(ii) the equation of PQ
(iii) the coordinates of the point where the line AB intersects the X-axis.
Find the equation of a line parallel to 2y = 6x + 7 and passing through (–1, 1).
