Advertisements
Advertisements
प्रश्न
Write down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.
उत्तर
Given, P divides the line segment joining A(−2, 6) and B(3, −4) in the ratio 2 : 3.
Co-ordinates of point P are
`((2 xx 3 + 3 xx (-2))/(2 + 3), (2 xx (-4) + 3 xx 6)/(2 + 3))`
= `((6 - 6)/5, (-8 + 18)/5)`
= (0, 2) = (x1, y1)
Slope of the required line = m = `3/2`
The required equation of the line is given by
y − y1 = m(x − x1)
`y -2 = 3/2 (x - 0)`
2y − 4 = 3x
2y = 3x + 4
APPEARS IN
संबंधित प्रश्न
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
Find the equation of the perpendicular dropped from the point (−1, 2) onto the line joining the points (1, 4) and (2, 3).
Find the equation of the line, whose x-intercept = 5 and y-intercept = 3
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = −23; and perpendicular to the line 4x – 2y = 1.
A line intersects x-axis at point (−2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
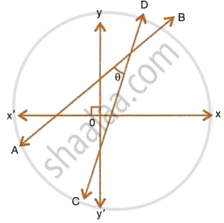
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = `sqrt(3)x - 1`. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
Find the value of a if the line 4 x = 11 - 3y passes through the point (a, 5)
Find the value of a line parallel to the following line:
`(2"x")/5 + "y"/3` = 2
A(8,5), B (-2,1) and C(5,4) are the vertices of a triangle. Find the equation of the median of the traingle through C.
Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
